from CSE142L.notebook import *
from notebook import *
# if you get something about NUMEXPR_MAX_THREADS being set incorrectly, don't worry.  It's not a problem.

Lab 4: The Memory Hierarchy (Part II)

Introduction

This lab is a continuation of the previous lab. While that lab focused on the basics of cache-aware programming and spatial locality, this lab will focus more on temporal locality and how you can modify your programs to maximize it.

As a reminder, between this lab and the last, you'll learn about the concepts of:

1. Memory alignment
2. Thinking in cache lines
3. Working sets
4. The cache hierarchy
5. The impact of miss rate on performance
6. The role of the TLB in determining performance
7. Spatial locality
8. Temporal locality
9. Cache-aware optimizations
10. The impact of data structures on memory behavior

Along the way, we'll address several of the "interesting questions" we identified in the first lab, including:

• Why does increasing the size of array change CPI? And why does this change occur so quickly?
• How and why do the datatypes we use change IC and CPI?
• Why does the order in which the program performs calculations affect CPI?

This lab includes a programming assignment.

Check the course schedule for due date(s).

Grading

Your grade for this lab will be based on the following components

Part	value
Reading quiz	3%
Jupyter Notebook	45%
Programming Assignment	50%
Post-lab survey.	2%

No late work or extensions will be allowed.

We will grade 5 of the "completeness" problems. They are worth 3 points each. We will grade all of the "correctness" questions.

You'll follow the directions at the end of the lab to submit the lab write up and the programming assignment through gradescope.

Please check gradescope for exact due dates.

New Tools

The only new tool you'll be using in this lab is a new kind of graph that visualizes a "trace" of memory accesses made by a program. Traces get used a lot in computer system analysis. In this case, it's a memory trace which is just a list of all of memory accesses a program makes.
We generate the trace using Intel's Pin binary instrumentation tool, which can do all kinds of cool things. In our case, it injects code into the running executable that writes the address of each load and store to a file along with some metadata (e.g., which thread made the access, whether it was read or write).

Here's an example:

The horizontal axis is the "access number". The first memory access in the program has access number 1, the second has access number 2, and so on. The vertical axis is the relative address. The colors mean different things in different plots.

You might ask "Why are these graphs janky screen captures?" Well, the graphs were rendered with a very cool Jupyter Notebook extension called Moneta that some of the first students to take 142L wrote as a group independent study during the spring of 2020 (the first quarter of the pandemic). It was an awesome interactive tool that let you pan and zoom and measure memory traces. However, it suffered from two key flaws:

1. It was entirely too much for datahub to handle. It used vast amounts of memory and would routinely crash students' virtual machines.
2. It relied on some obsolete python libraries.

Moneta II is in the works to address these problems, but it's not ready yet. So, for now, we have screen caps.

Temporal Locality

In the last lab, we examined the notion of spatial locality in detail. Now, we will turn to temporal locality.

Temporal locality exists when a program accesses the same memory multiple times within a short time. Caches exploit temporal locality by holding on to data that has been accessed recently. If the processor accesses it again, the cache can provide it very quickly.

With spatial locality, it was pretty easy to predict the cache miss rate for a simple loop that performs stride-based accesses (see below). With temporal locality it is harder because of associativity and conflicts. Before we dive into that, let's have quick refresher about how caches work (if this is fuzzy, go back and review the slides and/or readings from 142).

When a memory operation (load or store) accesses a memory location, $A$, the cache breaks $A$'s address into three parts:

tag	index	offset
the remaining bits	log2(# of associative sets)	log2(cache line size)

Together, the tag and the index of $A$ are a unique name (or number) for the cacheline-sized (and cacheline size-aligned) piece of memory that contains $A$. The index of $A$ tells the cache which associative set might contain that cache line.

The cache can then check that set to see if $A$ is present. If it is, it's a hit. If not, it's a miss, and the cache will choose one of the lines in the set to evict to make room for $A$'s cache line.

There are two important things to note:

1. $A$'s cacheline is in the cache if and only if, it is in the associative set corresponding to its index (it can never be in another associative set).
2. There are many, many other cache lines that also "live" in $A$'s associative set.

The L1 data cache in our processor is 32kB, with 64-byte lines, and it's 8-way set associative. So, there are 32,768/64 = 512 cache lines arranged in 512/8 = 64 associative sets. If the machine has 16GB of memory, it has 256-Million cache lines of main memory. So, there are about 4 million cache lines that "live" in each associative set. Clearly, there are plenty of opportunities for conflicts.

Working Sets

In lecture, you heard about the "working set" of an application, and the notion of a working set is deeply tied to temporal locality. The working set is the portion of memory that the program is currently using. The connection between working sets and temporal locality lies in the word "currently" since that refers to a period of time. In essence, the working set is the set of cache lines that a program accesses repeatedly over a period of time.

One thing to note: Without reuse, there can be no temporal locality. A single access to a cache line has no temporal locality.

Generally speaking, there will be fewer cache misses (and performance will be faster) if the working set fits in the L1 cache (or failing that, in the L2 cache).

  0%|          | 0/1 [00:00<?, ?it/s]

void working(uint64_t size) {
    auto s = new std::set<uint64_t>();
    uint64_t seed = 1;
    uint64_t sum = 0;

    for(uint x = 0; x < size; x++) {
        auto t = fast_rand(&seed);
        s->insert(t);
    }
    
    seed = 1;
    start_measurement();
    for(uint x = 0; x < size; x++) {
        auto a = s->find(fast_rand(&seed));
        sum += *a;
    }
    end_measurement();

    delete s;
}

Here's what the memory trace looks like

What you are looking at is the region of the heap that the C++ standard library is allocating to hold the set. Since, it's a tree-based structure, it's made up of many small objects that get allocated with new. The heap is allocating space starting at a low address and working upward -- hence the diagonal.

The color key is:

• Compulsory misses are light blue
• Hits are purple.
• Conflict misses are gold.

The Three C's

Recall from lecture (or review the slides) that we can classify cache misses into three types (known as "The Three C's"):

1. Compulsory: These misses occur because the processor has not accessed this cache line before.

2. Capacity: These occur because the program is accessing more memory than the cache can hold (i.e., it's working set is bigger than the cache).

3. Conflict: These occur because a given cache line of memory can only live in one of the associative sets of the cache.

Conflict Misses

Let's try to produce some conflict misses. In the last lab, we used a miss machine to generate lots of misses. They were mostly capacity misses (i.e., we accessed too many cache lines), and the miss machine let us produce lots of seemingly random accesses really fast. For conflict misses, we need something different: Highly-organized misses placed precisely.

The necessary ingredient for lots of conflict misses is many memory accesses that will map to the same associative set in the cache. If we access many of these cache lines, the associative set will "overflow" and that will causes misses.

Assume our 32kB cache with 64-byte lines and 8-way associativity and 64-bit addresses. Given an address $A$, how can we compute a new address, $B$, that will map to the same associative set but is not part of the same cache line as $A$? Given an index, $i$, into an array, how can we compute the index of another element, $j$, that will conflict with the first?

How do you compute B?

How do you compute j?

The main lesson here is that conflict misses are largely a product of bad luck if the working set is smaller than the cache: It may happen that for a particular cache capacity, associativity, and line size, that many cache lines in the application's working set happen to map to the same associative set.

Fortunately, in modern processors caches are pretty highly-associative (ours is 8-way) and at that level of associativity conflict misses are not a huge problem. If your working set is smaller than your cache's capacity, you'd have to be very unlucky to have enough cache lines land in the same associative set to cause many conflict misses. If your working set is larger than your cache, you're going to have misses regardless. As the example above shows, it is not hard to construct programs with small working sets that are unlucky. We have a term for these access patterns: We say they are "pathological".

By definition, pathological access patterns are rare, so we don't spend too much time worrying about them. But they can crop up and it's a good idea to be aware of the possibility.

The L2 and L3 Caches

So far in these two labs, we have focused on the L1 cache, but our machine also has L2 and L3 caches. Here's how they are organized:

As a reminder, the L1 is 32kB, 8-way set associative, with 64-byte lines. So, there are 512 cache lines divided into 64 associative sets.

The L1 and L2 are private to each core while the L3 is shared among all the cores on the CPU. The L2 is 256kB and is 8-way set associative. The L3 is 2MB per core, but it's shared across all the cores. Our machine has six cores, so 12MB.

On our machine, the L3 is the "last level cache" or LLC. The LLC is the cache just before DRAM. On some processors the LLC is the L2.

The TLB

The three levels of on-chip caches set the number of cache lines the processor can quickly access. As you heard in 142, though, there is another kind of cache in the processor: the TLB. Instead of data, the TLB caches the translations from virtual addresses to physical addresses, and its size sets the number of pages your program can access quickly.

Here's what our processor has:

1. 64 entries for 4kB pages (256kB total)
2. An L2 TLB with 1024 entries (8-way set associative; 4MBs total @ 4kB pages).
3. 32 entries for 2MB pages (64MB total).
4. 4 entries for 1GB pages (4GB total).

This is a little more complicated than what you heard about in 142. First off, there is an L1 TLB and an L2 TLB. If we think of the L1 TLB as cache for memory translations, then the L2 TLB is exactly analogous to the L2 cache: If the processor has a TLB miss in the L1 TLB, it can look in the L2 TLB. One important point: memory address translation always happens at the L1 cache because all the caches are physically tagged. This means that the L2 TLB has nothing to do with the L2 Cache.

The L2 TLB can cover 4MBs worth of 4kB pages of virtual address space. If you are using more pages than that, you'll get TLB misses and your performance will suffer.

Optimizing For Locality

Minimizing cache misses is critical for maximizing performance because, as you have seen, even a small number of misses can inflate CPI and ET. As a result, programmers who are concerned about performance often spend a lot of effort optimizing their code to reduce misses.

Below, we'll take a look a two common optimizations that aim to increase locality: Loop reordering and tiling.

In the compiler lab, you explored several other optimizations that compilers apply very effectively. While there are compilers that apply these (and other) locality optimizations, many do not, and even when they do, these locality optimizations do not work as effectively when applied automatically, so performance-obsessed programmers often apply locality optimizations by hand (but, of course, only when profiling and Amdahl's law demonstrates it's potentially profitable!).

Loop Renesting

Loop reordering or "re-nesting" is an optimization that changes the order in which loops are nested to improve locality. For instance, consider the code below. It initializes a 2D tensor, but it does it twice: The first time, the loop for x is on the outside of the loop nest. The second time, x is on the inside.

  0%|          | 0/1 [00:00<?, ?it/s]

#include"cfiddle.hpp"
#include"tensor_t.hpp"
#include"util.hpp"
#include<cstdint>

extern "C"
void x_inside(uint64_t size, uint64_t rows) {
    tensor_t<uint32_t> t(size/rows,rows,1,1);
    disable_prefetcher();
    flush_caches();
    start_measurement();
    for(uint y = 0; y < rows; y++) {
        for(uint x = 0; x < size/rows; x++) {
            t.get(x,y,0,0) = x;
        }
    }
    end_measurement();
    
}


extern "C"
void x_outside(uint64_t size, uint64_t rows) {
    tensor_t<uint32_t> t(size/rows,rows,1,1);
    disable_prefetcher();
    flush_caches();
    start_measurement();
    for(uint x = 0; x < size/rows; x++) {
        for(uint y = 0; y < rows; y++) {
            t.get(x,y,0,0) = x;
        }
    }
    end_measurement();
    
}


// Cfiddle-signature=c92a3c7647aabca719020bc299f5a6a8

Here's the memory trace for x_inside:

And here it is for x_outside():

Remarkably, those two plots contain exactly the same memory accesses, they are just distributed differently through time.

Recall from our earlier discussion of tensor_t, that incrementing the first argument to get() corresponds to moving to the next element in the underlying array of data. In the code above, x is the first argument to get(), so putting the x loop inside leads to better spatial locality.

You can see this reflected in the traces more clearly if we zoom in: With x on the inside, the program marches linearly through memory:

See how both the range of the horizontal and vertical axes are both quite small. This means that the accesses close in space and time.

With the x loop outside, it takes large strides through the array, and accesses to the addresses are spread out over a long time (note the much larger range on both axes:

In particular, it doesn't access the same 64 byte cache line again until long after it has been evicted from the cache.

Loop Tiling

Renesting loops can improve spatial locality, but it is generally less effective for improving temporal locality. There are two criteria that must be met in order to exploit temporal locality:

1. The cache line must be re-used.
2. The re-use must occur before the cache line is evicted by other cache lines coming in the cache.

This second condition has a direct connection to working set size: If the working set size of a piece of code is too large, it is likely that parts of it will be evicted before they are accessed again, making it hard for the processor to exploit the temporal and spatial locality.

Our goal, then, is to shrink the working set so that it fits in the cache and we can exploit the resulting locality.

Your programming assignment for this lab is to implement a memory allocator. You've used memory allocators a lot: in C++ you access them via new and delete. In C, it's malloc() and free() (which new and delete call internally). The default implementation of malloc() and free() are general purpose: they are reasonably fast and can allocate data of any size. However, many applications need to allocate many, many objects very quickly, so a general-purpose allocator is too slow. In these cases, it makes sense to implement a specialized memory allocator because they can be much faster.

In this lab, you'll be implementing a specialized memory allocator that has these basic characteristics:

1. It can only allocate objects of a single type (and therefore a single size). Allocators with this characteristic are sometimes called "slab allocators."
2. It will ensure those objects are aligned to a configurable size.
3. The allocator will be an object that can allocate and deallocate objects using a simple interface (see below).
4. When the allocator is deleted, it will automatically deallocated all objects that are still allocated.

Here's the reference implementation:

#include <stdlib.h>
#include <iostream>
#include <set>
#include <cstring>
#include "cfiddle.hpp"
#include"ChunkAlloc.hpp"

template<
	class T,          // This is the type we are allocating.  
		              // You can assume this is less than or equal to 4kB
	size_t ALIGNMENT  // The alignment at which we much allocate the objects.  
	                  // You can assume this is less than or equal to 4kB
	> 
class ReferenceAllocator {
	std::set<T*> chunks; // We store everything we allocated so we can clean up in the destructor.
public:
 	typedef T ItemType; // This will make T available as ReferenceAllocator::ItemType 
	static const size_t Alignment = ALIGNMENT;  // Likewise, we can access the alignment as 
	                                            // ReferenceAllocator::Alignment
	
	ReferenceAllocator() {}
	
        T * alloc() {
		void* p  = NULL;
		// this system call can allocate aribitrary-sized and aligned
		// objects.  Since it can handle any size, it's more general.
		int r =  posix_memalign(&p, ALIGNMENT, sizeof(T));
		if (r != 0) { 
			std::cerr << "posix_memalign() failed.  Exiting: " << strerror(r) << "(" << r << ")\n";
			exit(1);
		}
		
		// alloc_chunk provides void*, but we can assign to void.  So cast...
		uint8_t * t = reinterpret_cast<uint8_t*>(p);
		for(uint i= 0; i < sizeof(T); i++) {
			t[i] = 0; // and set to zero.
		}
		T* c = reinterpret_cast<T*>(p); // cast to the type we allocate.
		new (c) T; // This is the "in place" new operator.  
		           // It constructs an object at a given location.
		chunks.insert(c); // record it so we can delete it later.
		return c;
	}
	
	void free(T * p) {
		std::free(reinterpret_cast<void*>(p)); // Return the memory
		chunks.erase(p); // note that it's no longer allocated.
	}

	~ReferenceAllocator() {
		for(auto & p: chunks) { 
			std::free(reinterpret_cast<void*>(p)); // Return everything that still allocated.
		}
	}
};

template<class T, size_t ALIGNMENT> 
const size_t ReferenceAllocator<T, ALIGNMENT>::Alignment;

First, note that it's a template class that takes two parameters:

• T: the type it will allocate. You can assume the size of T no larger than 4096 bytes.
• ALIGNMENT: The alignment of the allocations it will make. Alignment size can be powers of 2 between 8 and 4096 bytes (8, 16, 32, 64, etc.).

The allocator has just four methods:

• ReferenceAllocator(): the constructor.
• alloc() allocates and returns an instance of T.
• free() deallocates p, a previously allocated instance of T.
• ~ReferenceAllocator(): The destructor for the allocator. It needs to clean up all the memory the allocator manages.

It also defines ReferenceAllocator::ItemType, which let's us access the type the allocator allocates and ReferenceAllocator::Alignment which gives us access to the alignment size.

The implementation above just relies on the standard library's alignment-aware interface to the general-purpose allocator (posix_memalign()). This means it's not optimized to exploit the fact that we only need to allocate a single size of object, and this is where the big optimization opportunities lie.

Your allocator will not rely on any of the normal memory-allocating library calls. Instead will use a very simple allocator to allocate memory in bulk from the operating system. The interface is called ChunkAlloc:

#define CHUNK_SIZE (128*1024)

extern void init_chunk(); // Set things up.
extern void * alloc_chunk(); // Allocate CHUNK_SIZE of memory
extern void free_chunk(void*p); // Free CHUNK_SIZE of memory
extern size_t get_allocated_chunks(); // Query how many chunks are currently allocated.

#include <stdlib.h>
#include<iostream>
#include <string.h>
#include "ChunkAlloc.hpp"
#include <sys/mman.h>

static size_t allocated_chunks = 0;

void init_chunk() {
	// This used to do stuff for Moneta. Now it's empty.
}

void * alloc_chunk() { // allocate CHUNK_SIZE bytes of memory by asking the operating system for it.
	
	// this is how malloc gets it's memory from the kernel.
	// mmap() can do many things.  In this case, it just asks the kernel to
	// give us some pages of memory.  They are guaranteed to contain zeros.
	void * r = mmap(NULL, CHUNK_SIZE, PROT_READ|PROT_WRITE, MAP_SHARED|MAP_ANONYMOUS, 0, 0); 
	if (r == MAP_FAILED) { 
		std::cerr << "alloc_chunk() failed. This often means you've allocated too many chunks. Exiting: " << strerror(errno) << "\n";
		exit(1);
	}
	allocated_chunks++; // This is just statistics tracking
	return r;
}

void free_chunk(void*p) { // Return the chunk to the OS.  After this, accesses to the addresses in the chunk will result in SEGFAULT
	int r = munmap(p, CHUNK_SIZE);
	if (r != 0) {
		std::cerr << "free_chunk() failed. exiting: " << strerror(errno) << "\n";
		exit(1);
	}
	allocated_chunks--;
}

size_t get_allocated_chunks() {
	return allocated_chunks;
}

ChunkAlloc gets memory the same way malloc() does: By calling the mmap() system call which stands for "memory map". mmap() is a great tool and can do many things. You can read about it here, but understanding it is not necessary for this lab. What is important for our purposes is that alloc_chunk() will return a 128kB region (or "slab" which how slab allocators got their name) of memory that is 4kB-aligned.

Detailed Requirements

You're going to build your own version of ReferenceAllocator called AlignedAllocator. You'll find a copy of ReferenceAllocator.hpp in AlignedAllocator.hpp. Do your work there.

Now that you understand the basics of how ReferenceAllocator works, here's the detailed list of requirements for AlignedAllocator:

1. All addresses that AlignedAllocator::alloc() returns must be aligned to ALIGNMENT so addr % ALIGNMENT == 0.
2. All addresses that AlignedAllocator::alloc() returns must point to at least sizeof(T) bytes of memory.
3. AlignedAllocator::alloc() needs to set all bytes of memory that the instance of T will occupy to zero before constructing T.
4. AlignedAllocator::alloc() needs to construct an instance of T in the memory using the in-place new operator (see below).
5. AlignedAllocator::alloc() cannot return the same pointer twice unless the pointer has been deallocated with AlignedAllocator::free() first.
6. After the destructor completes, AlignedAllocator must have called free_chunk() for every chunk it allocated with alloc_chunk(). i.e., get_allocated_chunks() must return 0.
7. You are free to use the STL data structures for the internals of AlignedAllocator, but alloc() may not return any memory that is a part of an STL container.
8. The only mechanism you can use to allocate memory is alloc_chunk()/free_chunk(). No calls to malloc() (or other functions from the standard library that allocate raw memory) or new (other than the "in place" version.) to allocate the space AlignedAllocator will return.
9. Your allocator must recycle: If memory is returned to it via free(), your allocator should reallocate that memory before requesting new memory via alloc_chunk(). This prevents your allocator from continually allocating new memory, which might be very fast, but not a realistic solution.

ReferenceAllocator already satisfies all of these except the last two: ReferenceAllocator uses posix_memalign() which is forbidden in your solution. With respect to recycling, I'm not sure how posix_memalign() works internally, so I'm not sure how it recycles, but it does something reasonably efficient. You'll find that removing posix_memalign() and meeting the above criteria will require you to rewrite most of the code in AlignedAllocator.hpp.

Evaluation

Your implementation will be evaluated based on correctness and performance. Your implementation of AlignedAllocator must pass the tests in run_tests.cpp which cover the requirements listed above. There will be hidden test cases.

The performance portion is based on the average score over several benchmarks in Allocator.cpp. Details of the grade calculation are given under "Final Measurement" below.

The code for the benchmarks is in Allocator.cpp. The code is below. The key functions are bench(), microbench(), exercise(), and miss_machine(). Here's what they do:

• microbench() just calls alloc() many times and records the execution time. Then it does the same for free().
• exercise() allocates a bunch of objects, deletes some at random, allocates some more, deletes some at random, etc. This puts your allocator into a "warmed up" or "well-used" state to approximate how it would behave in a long-running program.
• bench() measure the execution time of exercise().
• miss_machine() measures the speed of a specialized version of the miss machine that tests how well your allocator manages spatial locality (more below)

The *_solution functions near the bottom are wrappers to run each benchmark. Pay attention to where start_measurement() and end_measurment() are called.

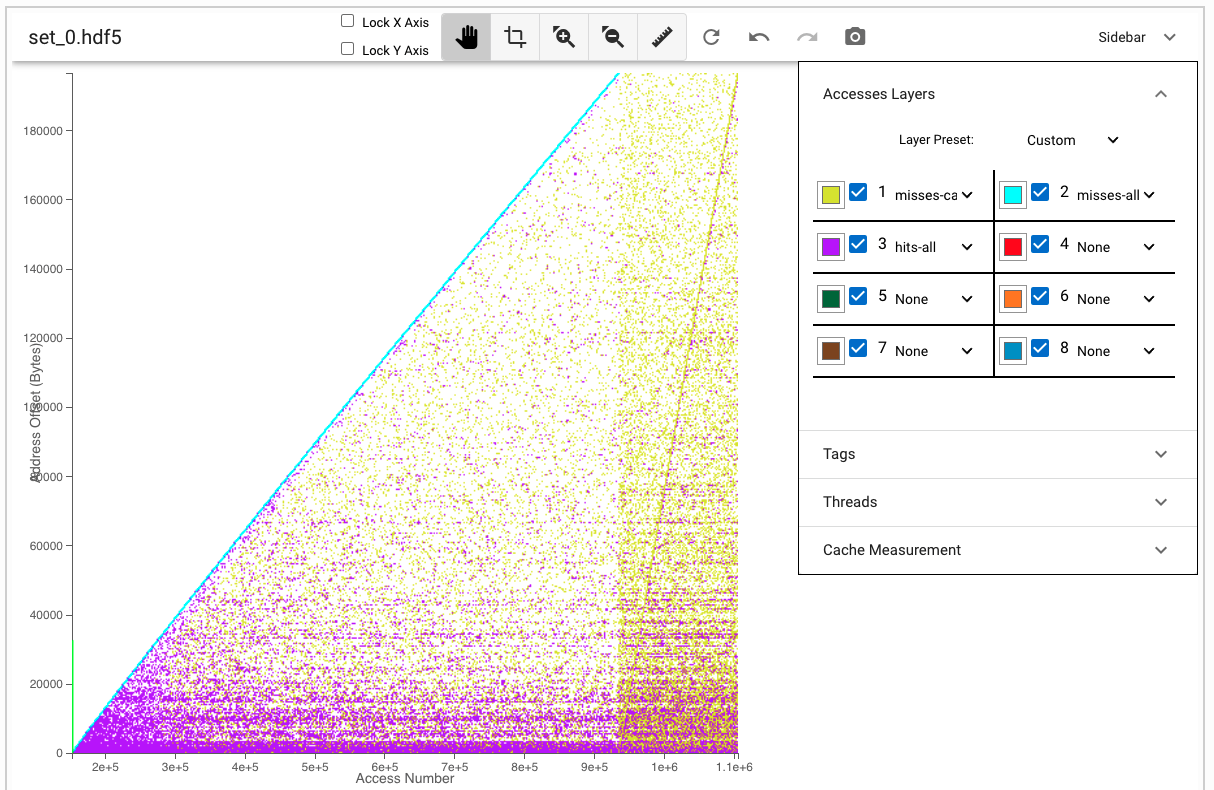
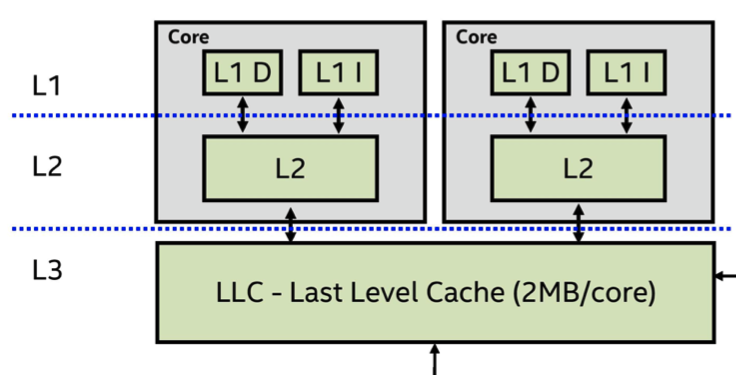
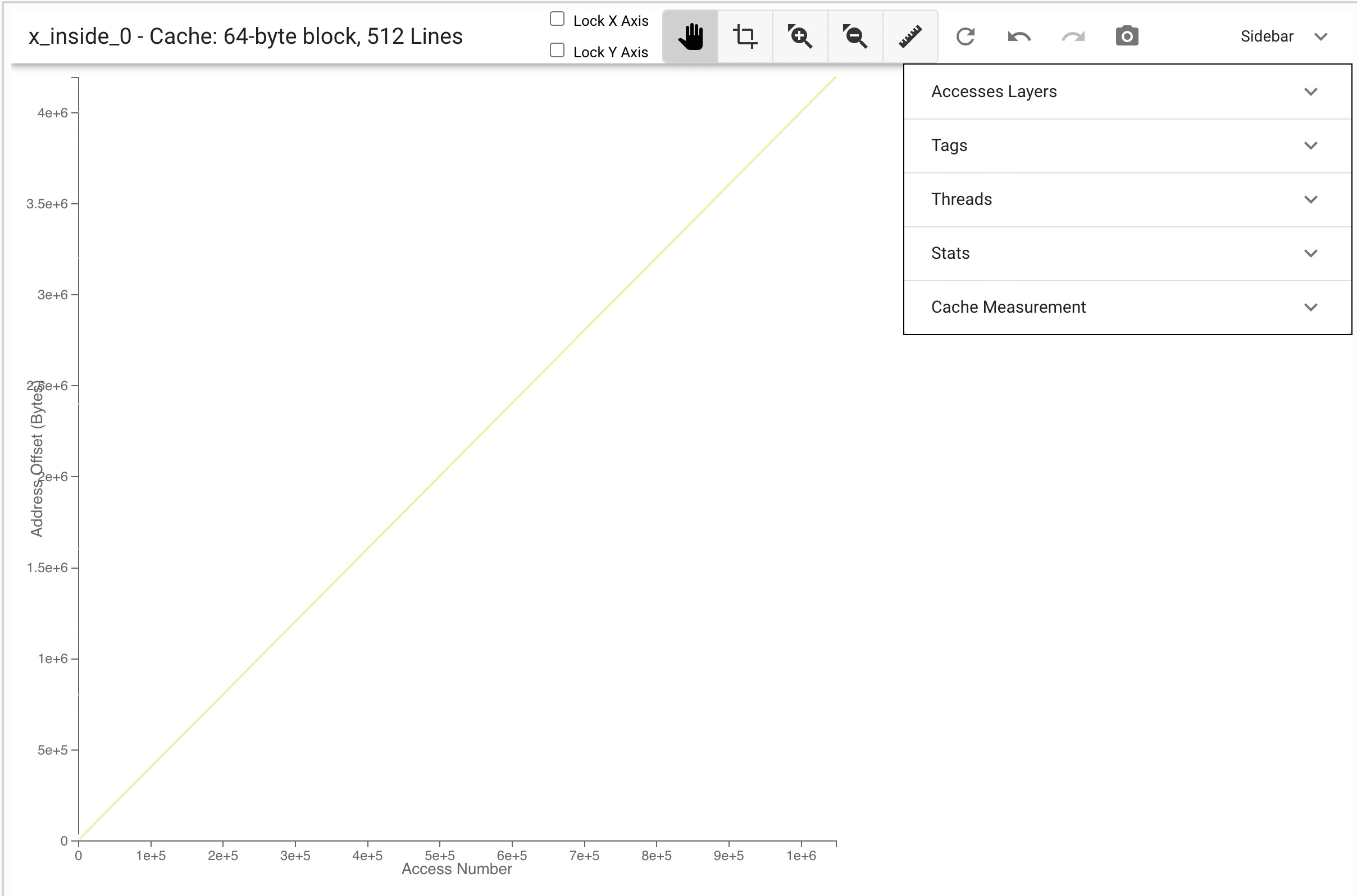
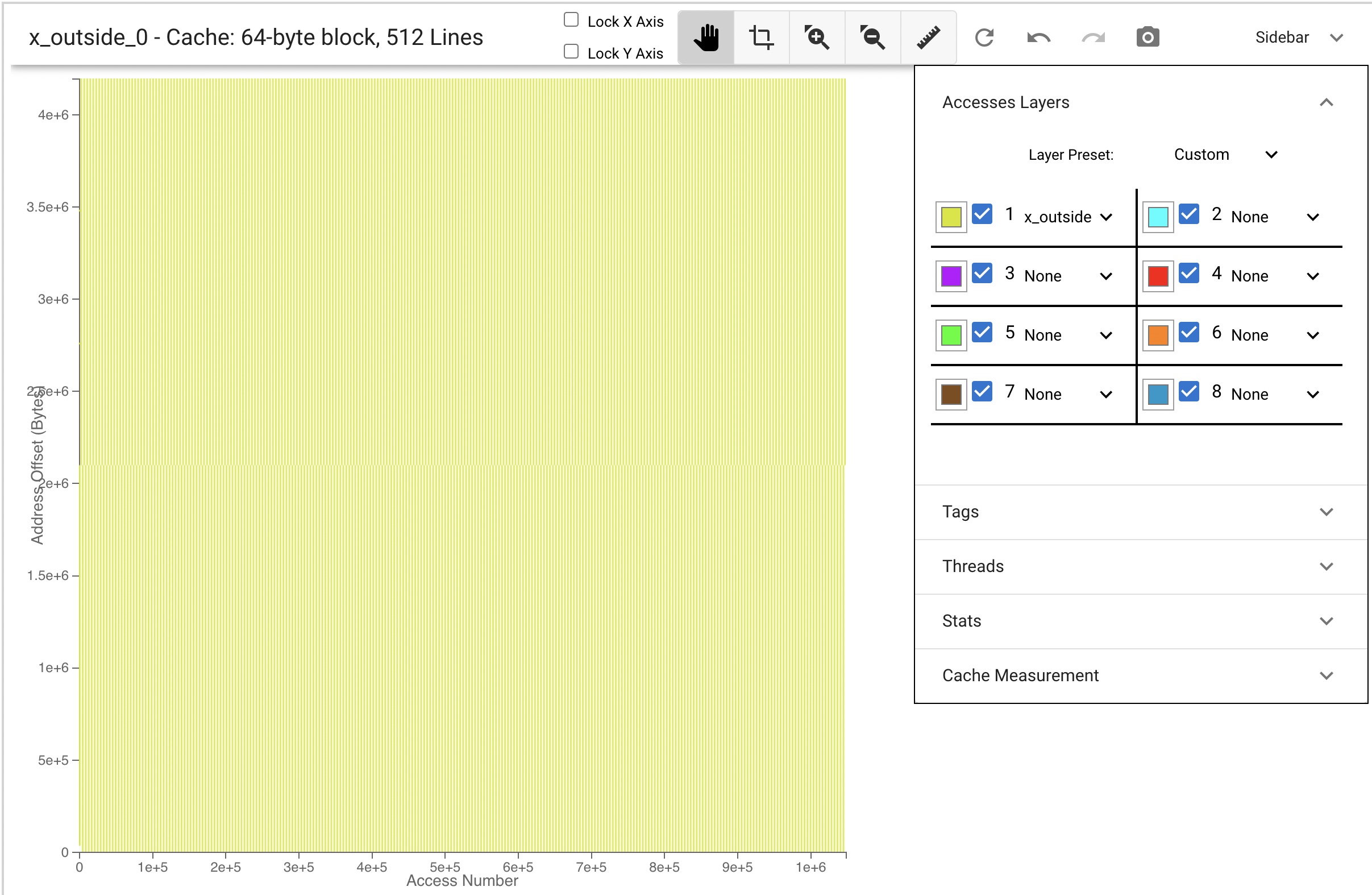
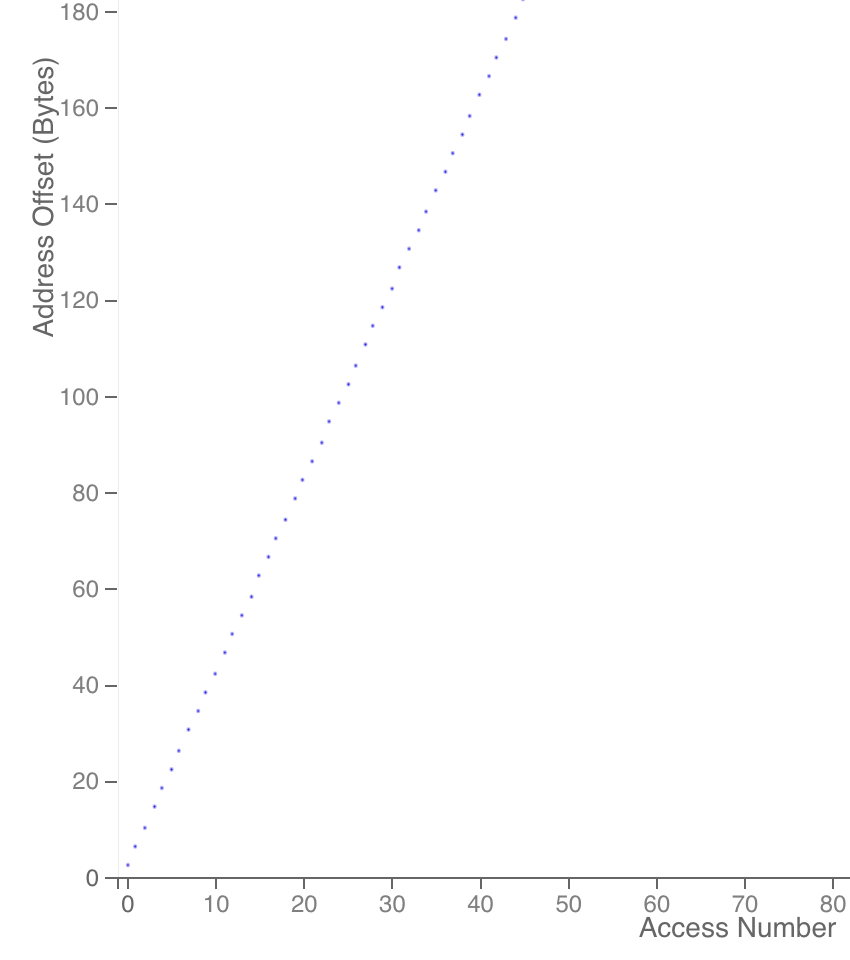
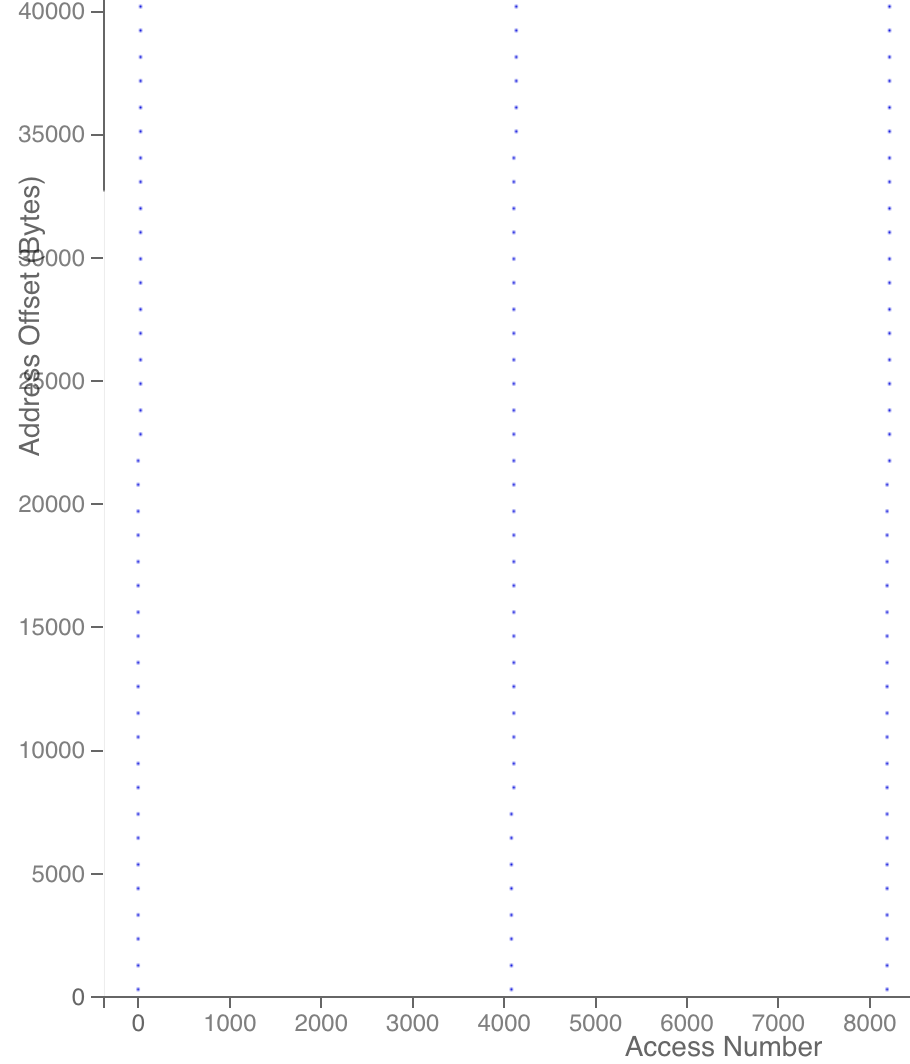
#include <stdlib.h>
#include<iostream>
#include"cfiddle.hpp"
#include<map>
#include<vector>
#include<algorithm>
#include"ReferenceAllocator.hpp"

#if USE_INSTRUCTOR_SOLUTION == 1
# include"admin/FastAllocator.hpp"
#else
# if USE_INSTRUCTOR_SOLUTION == 2
#  define ReferenceAllocator AlignedAllocator // This is terrible. I'm sorry.
#  include"ReferenceAllocator.hpp"
#  undef ReferenceAllocator
# else
# include"AlignedAllocator.hpp"
# endif
#endif

template<class Allocator>
void exercise(Allocator * allocator, size_t count, int iterations, uint64_t seed, bool cleanup = false) {
	// Interesting allocator behaviors an bugs emerge when the allocator
	// has to allocate and free objects in complex patterns.
	//
	// To simulate that, we allocate count items and then, on each
	// iteration, free about 1/4 of them and replace them with new items.
	
	std::vector<typename Allocator::ItemType *> items(count);
	
	for(unsigned int i = 0; i < count; i++)
		items[i] = NULL;

	for(int i = 0; i < iterations; i++) {
		for(unsigned int j = 0; j < count; j++) {
			if (items[j] == NULL) {
				items[j] = allocator->alloc();
			}
		}
		for(unsigned int j = 0; j < count; j++) {
			fast_rand(&seed);
			if (seed & 0x3) {
				allocator->free(items[j]);
				items[j] = NULL;
			}
		}
	}
	if (cleanup) {
		for(unsigned int j = 0; j < count; j++) {
			if (items[j]) {
				allocator->free(items[j]);
				items[j] = NULL;
			}
		}
	}

}


template<class Allocator>
void bench(uint64_t count, uint64_t seed, bool do_exercise, const char * tag) {
	auto alloc = new Allocator;
	if (do_exercise){ // warm it up.
		exercise<Allocator>(alloc, 4000, 20, seed);
	}
	start_measurement(tag);
	exercise<Allocator>(alloc, count/16, 16, seed);
	end_measurement();
	delete alloc;

}


template<class Allocator>
void microbench(uint64_t count, uint64_t seed, bool do_exercise, const char * alloc_tag, const char * free_tag) {

	auto alloc = new Allocator;
	
	if (do_exercise) { // get the allocator warmed up.
		exercise<Allocator>(alloc, 4000, 20, seed);
	}
	std::vector<typename Allocator::ItemType*> items(count);
	start_measurement(alloc_tag);
	for(uint64_t i = 0; i < count; i++) {
		items[i] = alloc->alloc();
	}
	end_measurement();
		
	if (do_exercise) {
		exercise<Allocator>(alloc, 4000, 20, seed);
	}
	start_measurement(free_tag);
	for(uint64_t i = 0; i < count; i++) {
		alloc->free(items[i]);
	}
	end_measurement();
	
	delete alloc;

}


//BEGIN
struct MissingLink {
	struct MissingLink * next;
};

extern "C"
struct MissingLink*  __attribute__((noinline)) do_misses(struct MissingLink * l, uint64_t access_count) {
	for(uint i = 0; i < access_count; i++) {
		l = l->next;
	}
	return l;
}

template<class Allocator>
void  miss_machine(uint64_t link_count, uint64_t access_count, uint64_t seed, const char * tag) {
	auto alloc = new Allocator; // create the allocator.

	exercise<Allocator>(alloc, 10000, 20, seed); // warm it up.

	std::vector<struct MissingLink *> links(link_count);  // Storage for the links
	for(auto &i : links) {                           // allocate them.
		i = alloc->alloc();
		i->next = NULL;
	}
	
	std::shuffle(links.begin(), links.end(), fast_URBG(seed));  // randomize the order of the links
	for(uint i = 0; i < links.size() -1; i++) { 
		links[i]->next = links[i+1];           // Make the next pointers reflect the ordering.
	}
	links.back()->next = links.front(); // complete the circle

	struct MissingLink * l = links[0];

	start_measurement(tag);
	l = do_misses(l, access_count); // Do the misses.
	end_measurement();

	delete alloc;

}
//END



// Call the starter code

extern "C"
void allocator_bench_starter(uint64_t count, uint64_t seed) {
	bench<ReferenceAllocator<uint8_t[3], 16>>(count, seed, true,      "bench-3-bytes"   );
	bench<ReferenceAllocator<uint8_t[125], 32>>(count, seed, true,    "bench-125-bytes" );
	bench<ReferenceAllocator<uint8_t[4096], 4096>>(count, seed, true, "bench-4096-bytes");
}


extern "C"
void allocator_microbench_starter(uint64_t count, uint64_t seed) {
	microbench<ReferenceAllocator<uint[4], 8>>(count, seed, true,       "alloc-4-bytes",    "free-4-bytes");
	microbench<ReferenceAllocator<uint[1024], 4096>>(count, seed, true, "alloc-1024-bytes", "free-1024-bytes");
}


extern "C"
void miss_machine_starter(uint64_t link_count, uint64_t access_count, uint64_t seed) {
	miss_machine<ReferenceAllocator<struct MissingLink, sizeof(struct MissingLink)> >(link_count, access_count, seed, "miss-machine");
}


// Call your code

extern "C"
void allocator_bench_solution(uint64_t count, uint64_t seed) {
	bench<AlignedAllocator<uint8_t[3], 16>>(count, seed, true,      "bench-3-bytes"   ); 
	bench<AlignedAllocator<uint8_t[125], 32>>(count, seed, true,    "bench-125-bytes" );
	bench<AlignedAllocator<uint8_t[4096], 4096>>(count, seed, true, "bench-4096-bytes");
}

extern "C"
void allocator_microbench_solution(uint64_t count, uint64_t seed) {
	microbench<AlignedAllocator<uint[4], 8>>(count, seed, true,       "alloc-32-bytes",    "free-32-bytes");
	microbench<AlignedAllocator<uint[256], 4096>>(count, seed, true, "alloc-1024-bytes", "free-1024-bytes");
}

extern "C"
void miss_machine_solution(uint64_t link_count, uint64_t access_count, uint64_t seed) {
	miss_machine<AlignedAllocator<struct MissingLink, sizeof(struct MissingLink)> >(link_count, access_count, seed, "miss-machine");
}

miss_machine()

miss_machine() is the most interesting of the three benchmark functions because it addresses one of the subtle problems that can arise with a memory allocator.

Because the memory allocator controls the layout of a program's memory, it can have a strong impact on how a program accesses memory. For instance:

1. If the allocator is poorly designed (or unlucky) it might arrange memory so that there are many conflict misses.
2. Depending on how effectively the allocator reclaims space that is freed, it may waste space.
3. How the allocator places objects can affect which objects are close enough to benefit from spatial locality.

The miss_machine() function in Allocator.cpp explores the third issue. Here's the code again:

  0%|          | 0/1 [00:00<?, ?it/s]

//BEGIN
struct MissingLink {
	struct MissingLink * next;
};

extern "C"
struct MissingLink*  __attribute__((noinline)) do_misses(struct MissingLink * l, uint64_t access_count) {
	for(uint i = 0; i < access_count; i++) {
		l = l->next;
	}
	return l;
}

template<class Allocator>
void  miss_machine(uint64_t link_count, uint64_t access_count, uint64_t seed, const char * tag) {
	auto alloc = new Allocator; // create the allocator.

	exercise<Allocator>(alloc, 10000, 20, seed); // warm it up.

	std::vector<struct MissingLink *> links(link_count);  // Storage for the links
	for(auto &i : links) {                           // allocate them.
		i = alloc->alloc();
		i->next = NULL;
	}
	
	std::shuffle(links.begin(), links.end(), fast_URBG(seed));  // randomize the order of the links
	for(uint i = 0; i < links.size() -1; i++) { 
		links[i]->next = links[i+1];           // Make the next pointers reflect the ordering.
	}
	links.back()->next = links.front(); // complete the circle

	struct MissingLink * l = links[0];

	start_measurement(tag);
	l = do_misses(l, access_count); // Do the misses.
	end_measurement();

	delete alloc;

}
//END

Here's what the benchmark does.

1. It create an allocator and warms it up with exercise().

2. It builds a miss machine out of links allocated one-at-a-time from your allocator. This is different than description of the miss machine given earlier in the lab: In that case we allocated the links in an array, guaranteeing good spatial locality.

3. Then it measures the execution time of a call to do_misses(), which traverses the miss machine.

Read through the code and comments carefully to understand it.

Useful C++

C++ likes to keep you safe by not letting you convert pointers to integers or letting you convert pointers from one type to another. However, memory allocators need to break the rules occasionally to transform untyped bytes into objects. The main tool for this is reinterpret_cast<>() and the "in place" new operator. ReferenceAllocator provides an example of how to use both mechanisms.

reinterpret_cast<>()

reinterpret_cast<>() let's you change a values from one type to another as long as they are the same size. So you can do this:

char *x;
int *y = reinterpret_cast<int *>(x);

// or 

void * x = alloc_chunk();
T * t = reinterpret_cast<T*>(x);

If you are familiar with C's (T*)(x) casting syntax, reinterpret_cast is equivalent, but preferred because it's easier to spot in code.

A related tool is uintptr_t, which is an unsigned integer that is the same size as a pointer. So you can increment a pointer by one byte doing this:

int * x = new int;
uintptr_t n = reinterpret_cast<uintptr_t>(x);
n += 1;
x = reinterpret_cast<int *>(n);

Note that this is different than;

int *x = new int;
x++;

Since, under C++'s pointer arithmetic rules, if you increment a pointer of type T*, it actually increases the address by sizeof(T) (i.e., 4 bytes for an int).

In-Place new

If you call new T, C++ will allocate some memory to hold a new instance of T and then run T's constructor on it. But what if you want to decide where to construct the new instance?

In that case you can say something like this:

void * p = alloc_chunk();
new (p) T;

To construct a new instance of T "in place" in the memory pointed to by p. Or, if you wanted to initialize an instance of T starting at the 11th byte after p, you could do this:

uintptr_t n = reinterpret_cast<uintptr_t>(p);
n += 11;
void *q = reinterpret_cast<void*>(n);
new (q) T;

Why would anyone ever want to do that?

How To Do This Lab

Here's some tips about how to approach this lab.

The Lifecycle of a Memory Allocator

Here are the basic steps that your memory allocator must accomplish over it's lifetime.

1. Initialize itself and its internal data structures.
2. Respond to calls to alloc()
   1. If the allocator has recycled objects, initialize one and return it.
   2. Otherwise, if the allocator has new (not recycled) memory on hand, initialize one object's worth and return it.
   3. Otherwise, if the allocator has no memory on hand, call alloc_chunk(), and goto 2.B.
3. Respond to calls to free()
   1. Store the object somewhere so it can be recycled.
4. On destruction, called free_chunk() to deallocate all the memory you allocated with alloc_chunk().

Thing to Try

Here are some ideas about how to get started:

1. The main difference between what you'll implement in AlignedAllocator and posix_memalign() is that AlignedAllocator only needs to allocate objects of a single size. You can exploit this fact to improve performance.
2. alloc_chunk() let's you allocate enough space to store many objects. Since the objects are all the same size and alignment, you can calculate where each of instance of T will reside with the chunk.
3. You need to recycle. So, think about how you can efficiently store free()ed memory while it's waiting to be re-alloc()ed.
4. You will need to choose the right data structures and algorithms to achieve good performance. Think about what each data structure needs to do and what operations are most important to performance. Use the STL! (In past labs, I noticed many students implementing things that the STL already provides. Don't re-invent -- or debug -- the wheel!)

Your overall score is based on your allocator's performance across eight benchmarks. This might seem daunting, but the performance of the benchmarks is very correlated: If you speed up your allocator for one of them, it will get faster for many of the others.

With that in mind, start with the simplest ones and go from there. I'd proceed in this order:

1. The microbench function.
2. The bench function.
3. The miss_machine function.

Checking Invariants to Find Bugs

Debugging your memory allocator can be challenging, because there are many opportunities to make mistakes and some errors (e.g., erroneously placing an object on your free list) may not cause a problem for long time. As a result, when the error is caught by the a regression test or a segmentation fault, the cause of the underlying problem might be very unclear.

A useful approach to debugging this kind of code is to focus invariants that your memory allocator should maintain. An invariant is a condition that should be true before and after the application calls any of methods of your allocator. For instance, here are some invariants that might hold for your allocator:

1. Every address you return to the application from alloc() should be aligned correctly.
2. A piece of memory should appear in the free list no more than once.
3. Every piece of memory that your allocator return should fit entirely within one of the chunks returned by AllocChunk().
4. No two pieces of memory you have allocated should ever overlap.
5. Every piece of memory that your allocator has ever returned should either be in the free list or currently allocated to the application.

Of these, 1 and 3 should hold for all allocators that correctly address the programming assignment, since they are restatements of the PA's requirements. The others happen to hold for my implementation. You should think about whether they apply to yours as well. They probably do, but the lab doesn't require it.

Invariants like these are useful because you can check them automatically and if you ever find that one of them is violated, then you know you have found a bug (either in your code or your invariant checker).

Let's look at how we could check the first invariant. I could implement my alloc() method like this (this is pseudocode):

#include<cassert>
T* alloc() {
    // Find the memory and initialized it, etc.

    assert(reinterpret_cast<uintptr_t>(r) % Alignment == 0);
    return r;

}

That would cause an assertion failure if I ever returned an incorrectly-aligned piece of data. If you haven't met assert() it's a very useful tool: It takes an expression and aborts the program if the expression is false.

That one is easy enough, but what about invariant 3? That's more complicated, but one approach would be to add a method to your allocator called check_invariants(). Here's what that function might do (again in pseudocode -- don't expect this to compile or be bug free):

void check_invariants() {
    for(c: my_chunks) {
        bool found = false;
        for(t: free_list) {
            if (the beginning of t is in c && the end of t is in c) 
                found = true;
        }
        assert(found);
    }
}

Now I can use check_invariants() like so:

T* alloc() {
    check_invariants();
    // Find the memory and initialized it, etc.

    assert(reinterpret_cast<uintptr_t>(r) % Alignment == 0);
    check_invariants();
    return r;

}

void free(T*) {
    check_invariants();
    // do stuff
    check_invariants();
}

You should call it at the end of the constructor and the beginning (and maybe end) of the destructor.

In fact, you might be able to call it after every line of your code to see where one of the invariants became broken.

Checking the other invariants is up to you.

But Won't This Make My Code Slow?

Definitely. It'll make it very, very slow. Which is why you only run it while debugging.

Here's useful trick:

//#define CHECK_INVARIANTS() // uncomment for production 
#define CHECK_INVARIANTS() check_invariants() // uncomment for debugging.

// other code

void free(T*) {
    CHECK_INVARIANTS();
    // do stuff
    CHECK_INVARIANTS();
}

Now you can turn all the checking on and off in one place and it costs zero performance when it matters.

Final Measurement

When you are done, make sure your best allocator is called AlignedAllocator in AlignedAllocator.hpp. Then you can submit your code to the Gradescope autograder. It will run the commands given above and compute your grade.

Your grade is based on your speed up relative ReferenceAllocator on the eight benchmarks.

For each of them, there's a target speedup given the table below.

You don't get extra credit for beating the targets. This will help ensure that your design in balanced: You must do well at all 8 benchmarks to do well on the lab.

To get points, your code must also be correct. The autograder will run the regressions in run_tests.cpp to check it's correctness. There are hidden tests.

You can mimic what the autograder will do with the command below, and then run the next cell below to list them and the target speedups.

After you run it, the results will be in autograde/bench.csv, autograde/microbench.csv, and autograde/miss_machine.csv rather than ./bench.csv, ./microbench.csv, and miss_machine.csv. This command builds and runs your code in a more controlled way by doing the following:

1. Ignores all the files in your repo except AlignedAllocator.cpp.
2. Copies those files into a clean clone of the starter repo.
3. Runs your code using run_bench.py
4. It then runs autograde.py to compute your grade.

Running the cell below will do the same thing as the Geradescope autograder. And the cell below shows the name and target speedups for each benchmark. This takes a few minutes to run.

Recap

This lab completes our tour of (single processor) memory systems. It explored what's required to exploit temporal locality and when it does and does not exist. It also looked at other key components of the memory hierarchy: The lower-level caches and the TLB. Finally, it developed an optimized version of 1-D convolution using tiling and renesting. You should now be well-prepared for the next lab, where we will explore (among other things) how multiple processors further-complicate the performance of the memory hierarchy.